Basic Algebra Formulas
(a+b)2 = a2 + b2 + 2ab
(a-b)2 = a2 + b2 – 2ab
(a+b) (a-b) = a2 – b2
(x + a)(x + b) = x2 + (a + b)x + ab
(x + a)(x – b) = x2 + (a – b)x – ab
(x – a)(x + b) = x2 + (b – a)x – ab
(x – a)(x – b) = x2 – (a + b)x + ab
(a + b)3 = a3 + b3 + 3ab(a + b)
(a – b)3 = a3 – b3 – 3ab(a – b)
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2xz(x + y – z)2 = x2 + y2 + z2 + 2xy – 2yz – 2xz
(x – y + z)2 = x2 + y2 + z2 – 2xy – 2yz + 2xz
(x – y – z)2 = x2 + y2 + z2 – 2xy + 2yz – 2xz
x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy –yz -xz)
x2 + y2 =½ [(x + y)2 + (x – y)2]
(x + a) (x + b) (x + c) = x3 + (a + b +c)x2 + (ab + bc + ca)x + abc
x3 + y3= (x + y) (x2 – xy + y2)
x3 – y3 = (x – y) (x2 + xy + y2)
x2 + y2 + z2 -xy – yz – zx = ½ [(x-y)2 + (y-z)2 + (z-x)2]
Product of rational numbers = (Product of Numerators) / (Product of Denominators)
First Rational Number × (Reciprocal of other Rational Number)
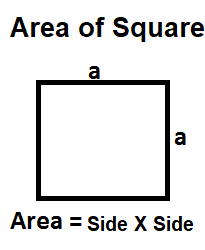
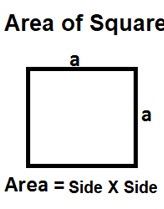
Area of a Square = Side2
Perimeter of a Square = 4 × Side
Area of Rectangle = Length × Breadth
Perimeter of a Rectangle = 2 × (Length + Breadth)
Area of a Parallelogram = Base × Height
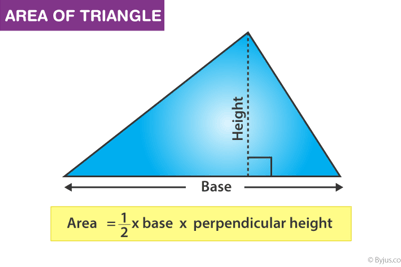
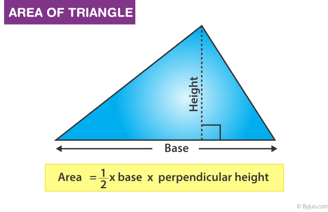
Area of Triangle = 1/ 2 × Base × Height
Circumference of a Circle = π d, where ‘d’ is the diameter of a circle and π = 22/7 or 3.14
Area of a Circle = πr2
Increase in Percentage = (Change / Original
Amount) × 100
Profit Percentage = (Profit / Cost price) × 100
Simple Interest = (Principal × Rate × Time) / 100
Amount = Principal + Interest
Additive inverse of rational number: a/b = -b/a
Multiplicative Inverse of a/b = c/d , if a/b × c/d = 1
Probability of the occurrence of an event = Number of outcomes that comprise an event/ Total number of outcomes
Compound Interest formula = Amount – Principal, Amount in case the interest is calculated annually = Principal ( 1 + Rate/100)n, where ‘n’ is the period.
1. Real Numbers
√ab = √a √b
√(a/b) = √a / √b
(√a + √b) (√a – √b) = a – b
(√a + √b)2 = a + 2√ab + b
(a + √b) (a – √b) = a2 – b
(a + b) (a – b) = a2 – b2
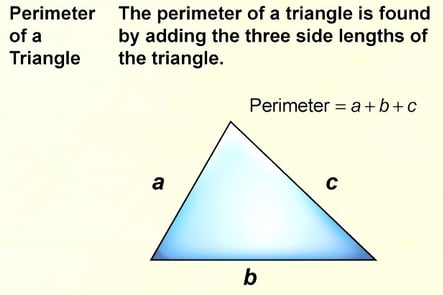
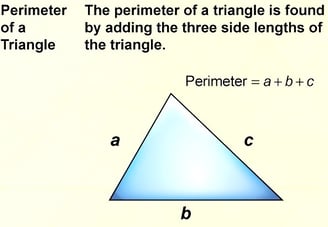


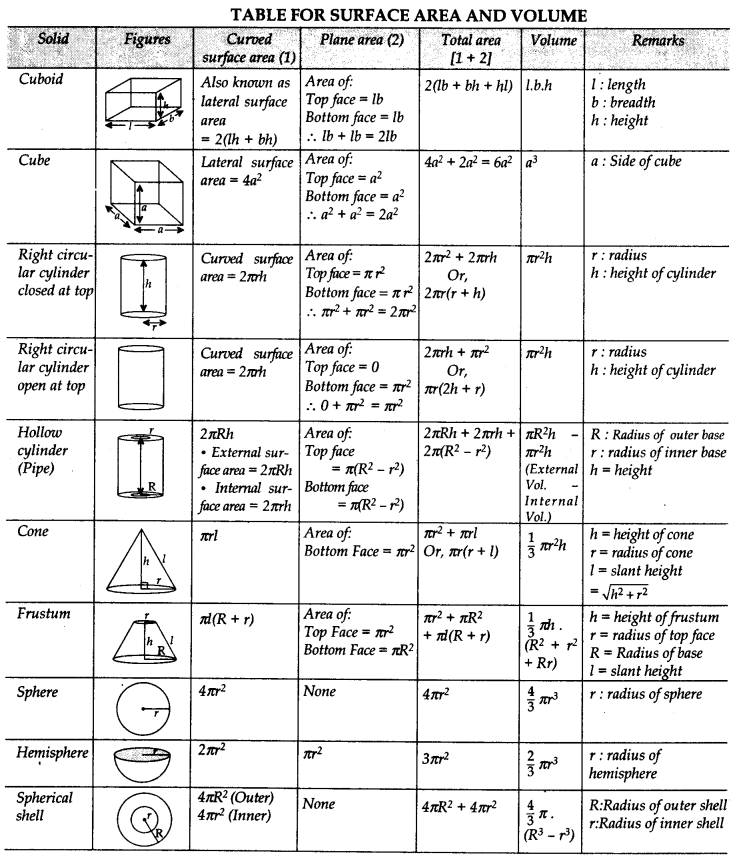
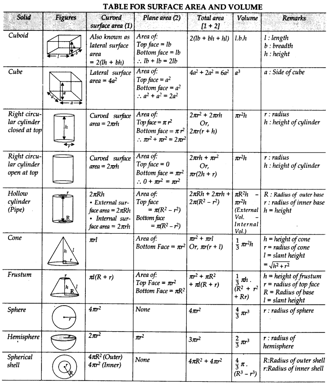
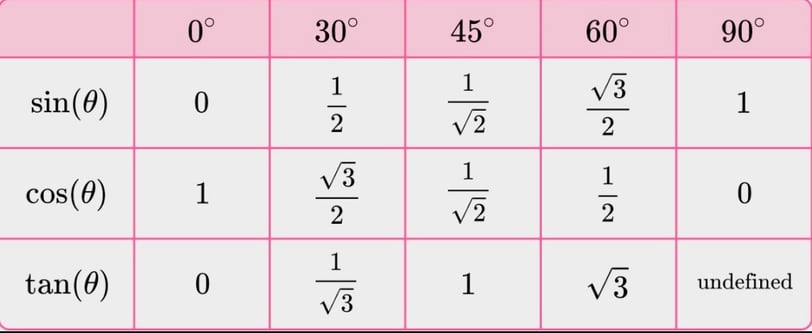
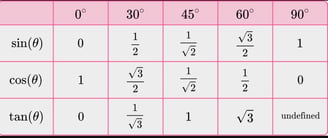
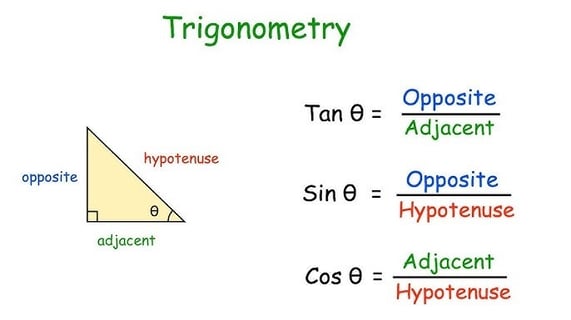
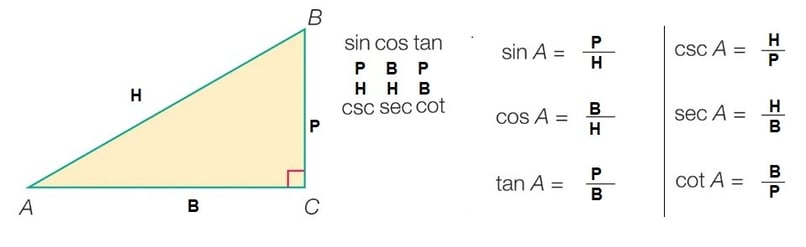
Trigonometry
sin(90° – A) = cos A
cos(90° – A) = sin A
tan(90° – A) = cot A
cot(90° – A) = tan A
sec(90° – A) = cosec A
cosec(90° – A) = sec A
sin2 θ + cos2 θ = 1
cosec2 θ – cot2 θ = 1
sec2 θ – tan2 θ = 1
BODMAS FORMULA
B (Brakets)
O ( Off )
D ( Divide )
M ( Multiply )
A ( ADD )
S ( SUBTRACT )
